
Séminaire d’Eté sur « l’Objet de la Psychanalyse » (août-sept 2002, Paris)
Dans le séminaire « L’Objet de la psychanalyse », Lacan se réfère à plusieurs reprises à Girard Desargues pour marquer l’avancée spécifique effectuée par celui-ci par rapport aux techniques développées par les peintres du XVe siècle pour mettre en place la science de la perspective. Il m’a paru utile de donner un aperçu plus précis de cette avancée. En effet – c’est une hypothèse qui m’a été suggérée par Jean-Paul Hiltenbrand et que je vais tenter de soutenir – il me semble qu’il existe une profonde analogie entre d’une part ce qu’a réalisé Desargues en partant des techniques de la perspective, et en fondant la géométrie projective, et d’autre part ce que Lacan tente dans ce séminaire en abordant l’objet regard sous son angle symbolique, en particulier dans les leçons XVI et XVII. J’espère pouvoir illustrer que, de même que Lacan nous montre que la structure sous-jacente du fantasme implique un sujet divisé d’une part, un objet perdu de l’autre, Desargues nous montre que la structure sous-jacente du dispositif de la perspective implique l’existence, déduite d’une pure construction discursive, d’un point unique, radicalement perdu en ceci qu’il ne peut en aucun cas être visualisé directement.
Nous connaissons peu de chose de la biographie de Girard Desargues. L’essentiel peut en être trouvé dans l’ouvrage de R. Taton (L’œuvre mathématique de Girard Desargues, PUF 1951) et dans l’ouvrage collectif réalisé sous la direction de G. Dhombres. On sait que, de 5 ans l’aîné de Descartes, il entretint avec ce dernier des relations d’estime réciproque, et qu’il fréquentait assidûment le cercle de scientifiques rassemblés autour du Père Mersenne entre 1630 et 1650. Géomètre respecté, il fut cependant, comme l’indique Lacan, l’objet d’attaques virulentes dès 1640, attaques visant principalement à contester l’originalité de ses méthodes.
Pour illustrer l’esprit de la démarche de Girard Desargues, il me semble indiqué de citer un bref passage de l’un de ses écrits : une lettre à Mersenne datant de l’époque (1638) où il rédigeait son ouvrage le plus novateur, le « Brouillon projet d’une atteinte aux événements de rencontre du cône avec un plan » . Dans cette lettre, il répond à Mersenne, qui lui demandait d’arbitrer une controverse entre Fermat et Descartes, concernant la meilleure manière de mener les tangentes d’un point à une parabole. Il écrit : « …par mes contemplations capricieuses du cône rencontré par divers plans en toutes façons et des lignes et des figures qui s’engendrent en cette rencontre, j’ay trouvé que par une seule et mesme énonciation, construction et préparation, ou pour dire mieux par un seul et mesme discours et sous de mesmes paroles, on déclare un moyen de construire ou bien on déclare les moyens de faire une construction d’un autre ordre par laquelle on voit également une pareille génération, en toutes espèces de plates coupes de cônes, de toutes espèces de lignes droites … ». Cette citation pourrait parfaitement passer pour l’acte fondateur de la géométrie projective, à savoir l’étude des propriétés des figures que se conservent par projection, et qui peuvent donc s’énoncer par un seul et même discours. Ainsi, la transformation de la perspective, qui transforme (par exemple) un cercle dans la réalité en une ellipse sur le tableau, Desargues va s’en servir de manière extensive et abstraite pour en quelque sorte exporter les propriétés du cercle à toutes espèces de « plates coupes du cône », ellipses, paraboles, hyperboles, ou même couples de droites concourantes ou parallèles. Une illustration de cette généralisation est donnée figure 1 : le théorème dit de l’hexagramme mystique de Pascal, dual du théorème de Brianchon, cité par Lacan, est valable aussi bien pour une ellipse que pour une hyperbole.

| Figure 1 : Le théorème de l’Hexagramme mystique de Pascal : « Les côtés opposés d’un hexagone quelconque inscrit dans une conique se coupent selon trois points alignés » est vrai pour une ellipse aussi bien que pour une hyperbole. L’un des cas se déduit de l’autre par la transformation projective définie par Desargues. |
Une conséquence importante de cette volonté de Desargues de bâtir un discours unique qui rende compte des propriétés de toutes les coniques est qu’il est amené « tout naturellement » à considérer que des droites parallèles se coupent en un point ordinaire. Ainsi, dès l’introduction du Brouillon projet, il pose : « pour donner à entendre de plusieurs lignes droites qu’elles sont toutes entre elles ou bien parallèles ou bien inclinées à même point, il est ici dit que toutes ces droites sont d’une même ordonnance entre elles. L’endroit auquel on conçoit que tendent ainsi plusieurs droites en l’une aussi bien qu’en l’autre de ces deux espèces de position est ici nommé but de l’ordonnance de ces droites. ». La même généralisation est utilisée pour les ordonnances de plans « parallèles ou inclinés à mesme droite », et « l’endroit auquel on conçoit que tendent ainsi plusieurs plans en l’une aussi bien que l’autre de ces deux espèces de position a ici nom essieu de l’ordonnance de ces plans ».
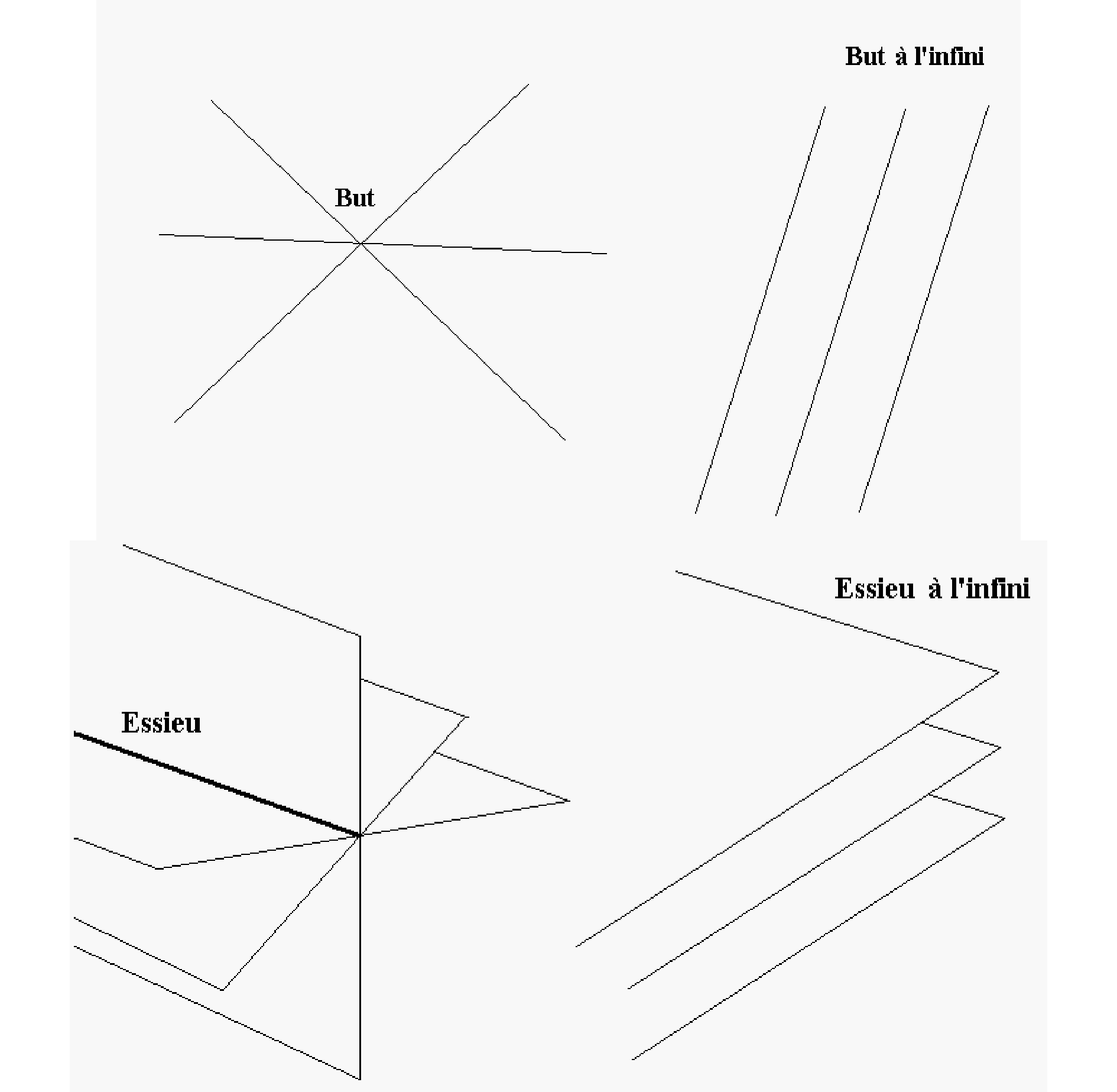
| Figure 2 : les divers types d’ordonnances de droites et de plans selon Desargues. |
La figure 2 illustre ces définitions. On voit que l’essieu dans le cas d’un faisceau de plans, est simplement la droite commune à ces plans. Ce n’est que pour un faisceau de plans parallèles que l’essieu est rejeté à l’infini, et devient donc moins facile à concevoir. Sur cette banalisation du point à l’infini, Desargues s’explique peu. Il se contente d’écrire :
« Chacun pensera ce qui luy semblera convenable ou de ce qui est icy déduit, ou de la manière de le déduire, et verra que la raison essaye à connaître des quantités infinies d’une part ; ensemble des si petites que leurs deux extrémités opposées sont unies entre elles, & que l’entendement s’y pert, non seulement à cause de leur inimaginables grandeur & petitesse, mais encore à cause que le raisonnement ordinaire le conduit à en conclure des propriétés dont il est incapable de comprendre comment c’est qu’elles sont. »
On ne saurait mieux définir la démarche purement symbolique du mathématicien : La raison le mène là où l’entendement se perd, parce que c’est inimaginable et qu’on ne comprend pas comment cela peut être. N’est-ce pas une démarche semblable qu’entreprend Lacan lorsqu’il nous mène à concevoir cet objet dont J.-P. Hiltenbrand nous a rappelé qu’il est représenté, mais non représentable ? On peut remarquer au passage que ce que nous propose Desargues revient à remplacer l’axiome d’Euclide : « Par un point extérieur à une droite D, il passe une et une seule parallèle à D » par le suivant : « Par deux points il passe une droite et une seule ; Deux droites se coupent (toujours !) en un point et un seul ». Il fonde donc en toute rigueur une géométrie non-euclidienne, ou du moins plus tout à fait euclidienne.
Je voudrais maintenant donner un exemple de cet in-imaginable auquel mène la raison de Desargues, lorsqu’il l’applique au dispositif habituel de la perspective. En effet, c’est en suivant pas à pas cette généralisation que Lacan va nous amener à concevoir l’objet regard comme nécessaire, tout en nous montrant l’impossibilité qu’il y a à l’imager.
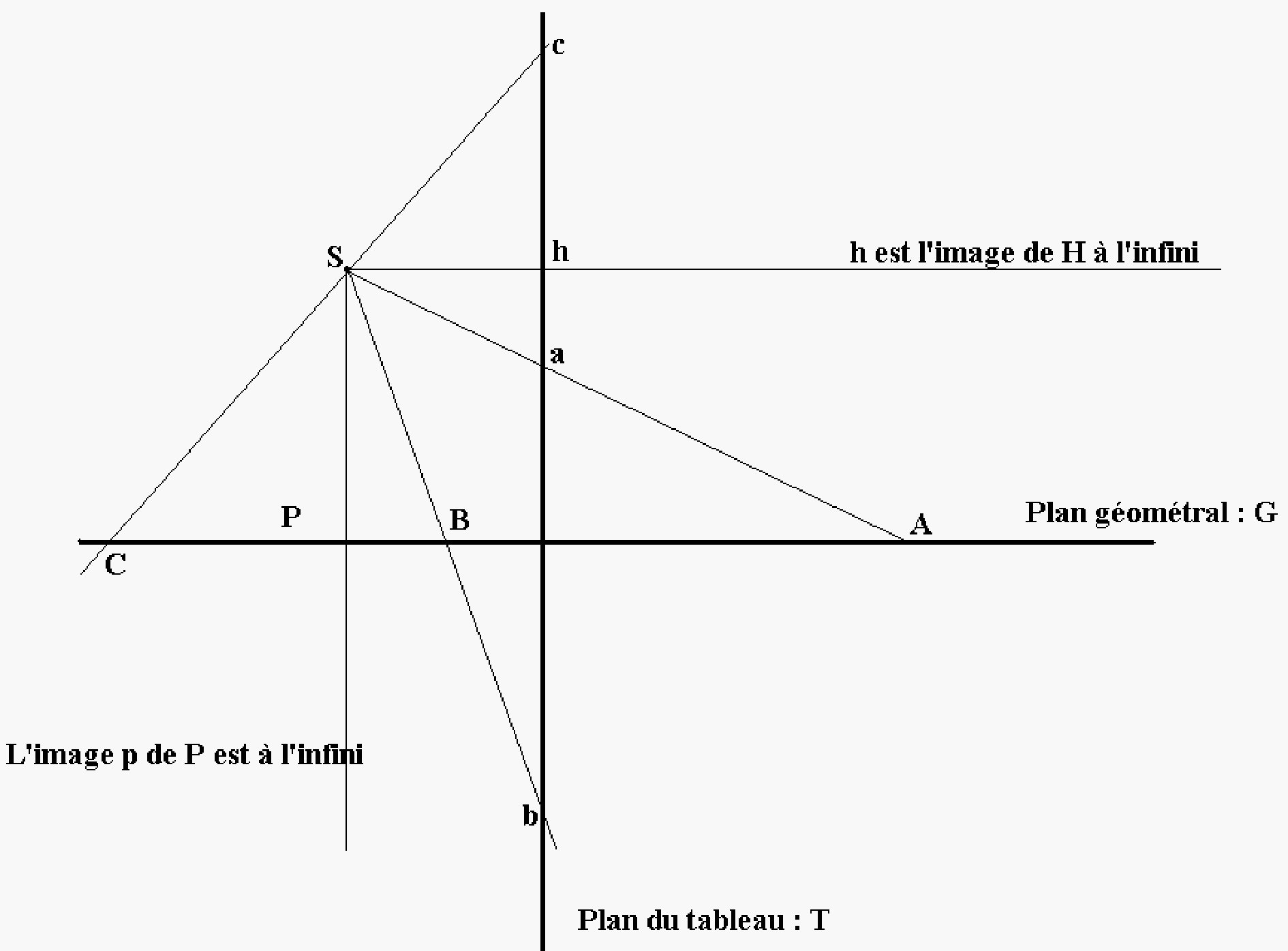
| Figure 3 : Le dispositif de la perspective, vu de profil. |
Si nous considérons le dispositif vu de profil (figure 3), tel que Desargues le purifie, il se réduit à deux plans : le plan géométral G, et le plan du tableau T, eux mêmes représentés par deux droites. Le sujet se réduit au point S, sommet de la pyramide visuelle pour les perspecteurs, but d’une ordonnance de droites pour Desargues (cette distinction est importante, et Lacan la souligne). La transformation projective consiste à associer à un point A du plan géométral son image a du tableau : a est l’intersection de la droite SA avec le plan T. Mais là où Desargues subvertit le dispositif des perspecteurs, c’est quand il applique cette définition à la lettre. En effet, s’il paraît « naturel » de faire de a l’image de A (voir figure 3) lorsque A est situé devant le sujet et au delà du plan du tableau, il l’est déjà beaucoup moins de faire de b l’image de B, lorsque B est situé entre le sujet et le tableau. Lacan parle à ce sujet de « profondeurs infinies ». En effet, lorsque B s’approche des « pieds » P du sujet son image b s’éloigne infiniment vers le bas sur le plan du tableau. Le moment où le dispositif arguésien s’éloigne définitivement des perspecteurs est celui où, continuant à appliquer à la lettre la transformation perspective, il en déduit que l’image d’un point C situé derrière le sujet a également son image c dans le plan du tableau. C’est à ce propos que Lacan s’exclame : « Et au dessus de l’horizon, vous allez dire naturellement le ciel ? mais pas du tout, pas du tout, pas du tout, …». En continuant cette démarche, il apparaît également que le point h du tableau n’est l’image d’aucun point visible du plan géométral. C’est ce qui conduit Desargues à poser l’existence d’un point H (à 3 dimensions, une ligne) du géométral, l’horizon, auquel on n’a accès que via son image h. De même le point P du géométral (les « pieds » du sujet) n’a pas d’image visible. Desargues pose néanmoins qu’il en a une, le point p, à l’infini du tableau dans cette direction.
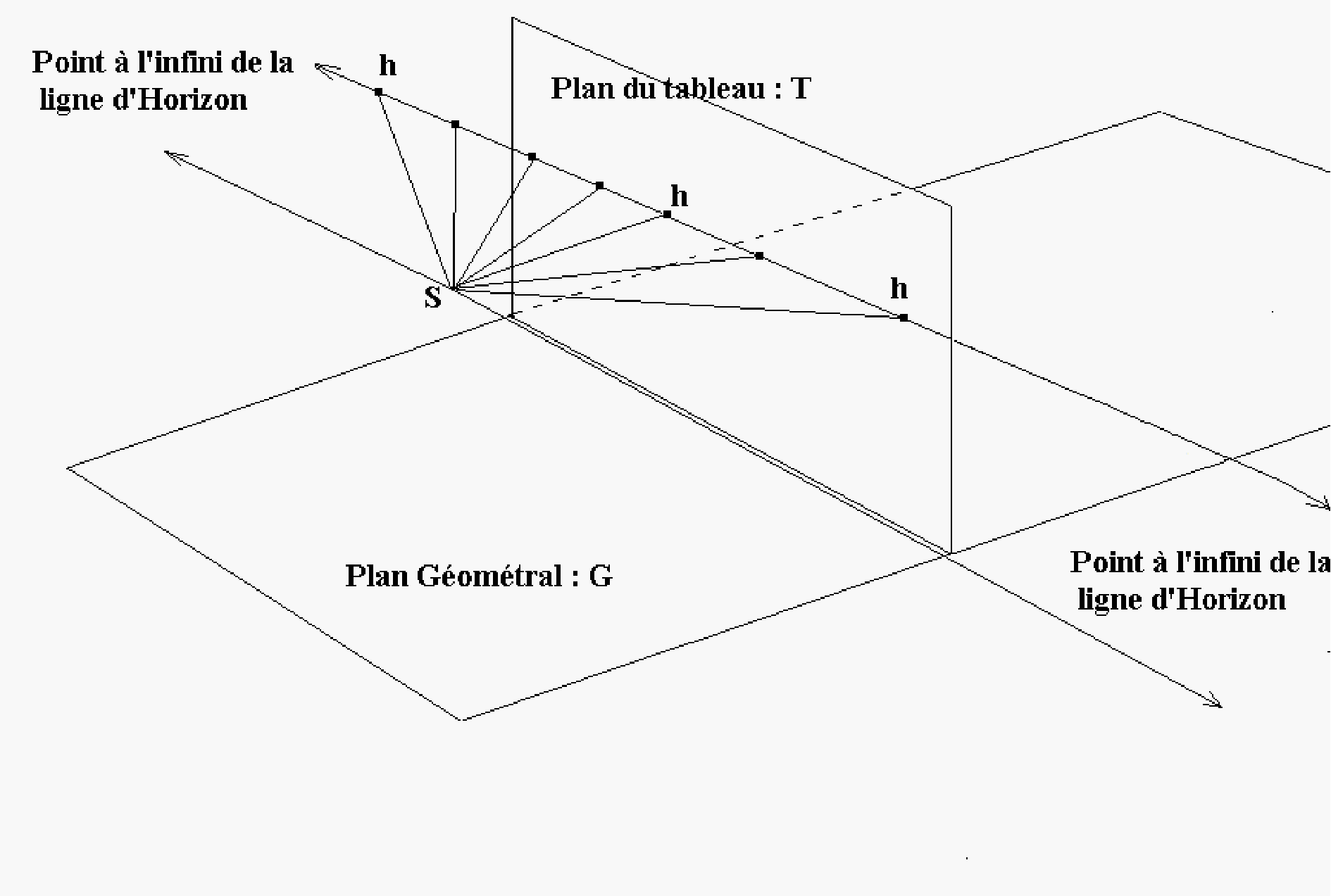
| Figure 4 : Le point à l’infini de la ligne d’horizon n’est visible ni dans le plan du tableau ni dans le plan géométral. Pourtant, il appartient aux deux : c’est l’intersection des lignes à l’infini de G et T. |
Si l’on examine maintenant le dispositif à 3 dimensions (figure 4), on s’aperçoit rapidement, par un raisonnement identique, que tous les points h de l’horizon du tableau sont les images de points H du géométral qui ne sont pas représentables. Leur existence est là encore posée par Desargues, comme constituant la droite à l’infini du plan géométral. C’est cette droite dont Lacan souligne que les géomètres grecs l’ont « ratée ». C’est une droite, nous dit Lacan, que nous pouvons concevoir comme faisant le tour du plan géométral. Mais il y a plus : la 3e dimension fait apparaître un point, le point à l’infini de l’horizon lui-même, point appartenant à la fois au plan du tableau et au plan géométral, qui n’est visible ni dans l’un ni dans l’autre. Ce point unique, que tout le raisonnement de Desargues nous amène à concevoir, est littéralement le point perdu de la perspective : le raisonnement nous y conduit, mais notre entendement, notre vision, le perd. A l’instar de l’objet regard, il s’avère représenté (dans le système symbolique de la géométrie projective), mais pas représentable dans la figure du dispositif.
Lacan attire notre attention sur le fait que ce point se trouve sur l’essieu commun au plan du sujet (le plan parallèle à T passant par S) et au plan du tableau. Cette remarque prend son poids du fait que Lacan souligne également, dans une leçon précédente, que pour nous, il n’est pas possible de souscrire à la division posée par Descartes entre substance pensante et substance étendue. Le point perdu de la perspective est en effet conçu par Desargues comme se trouvant à la fois dans l’espace occupé par le peintre et dans celui où se trouve le tableau, interdisant ainsi de poser ces deux espaces comme hétérogènes.
Il me paraît important de noter que dans les leçons XVI et XVII, lorsque dans sa démonstration, Lacan nous conduit pas à pas vers ce point, il associe toujours à sa démonstration, souvent dans la même phrase, la nécessité de retrouver dans le tableau non pas une, mais deux références au sujet, qui sont le point de fuite principal et le point de distance. Cettte observation me semble difficile à interpréter, sinon comme un signe s’il en était besoin, du fait que Lacan, dans sa démarche visant à cerner l’objet regard, s’appuie en permanence sur la formule du fantasme : un sujet divisé, double, et un objet, inconcevables l’un sans l’autre.
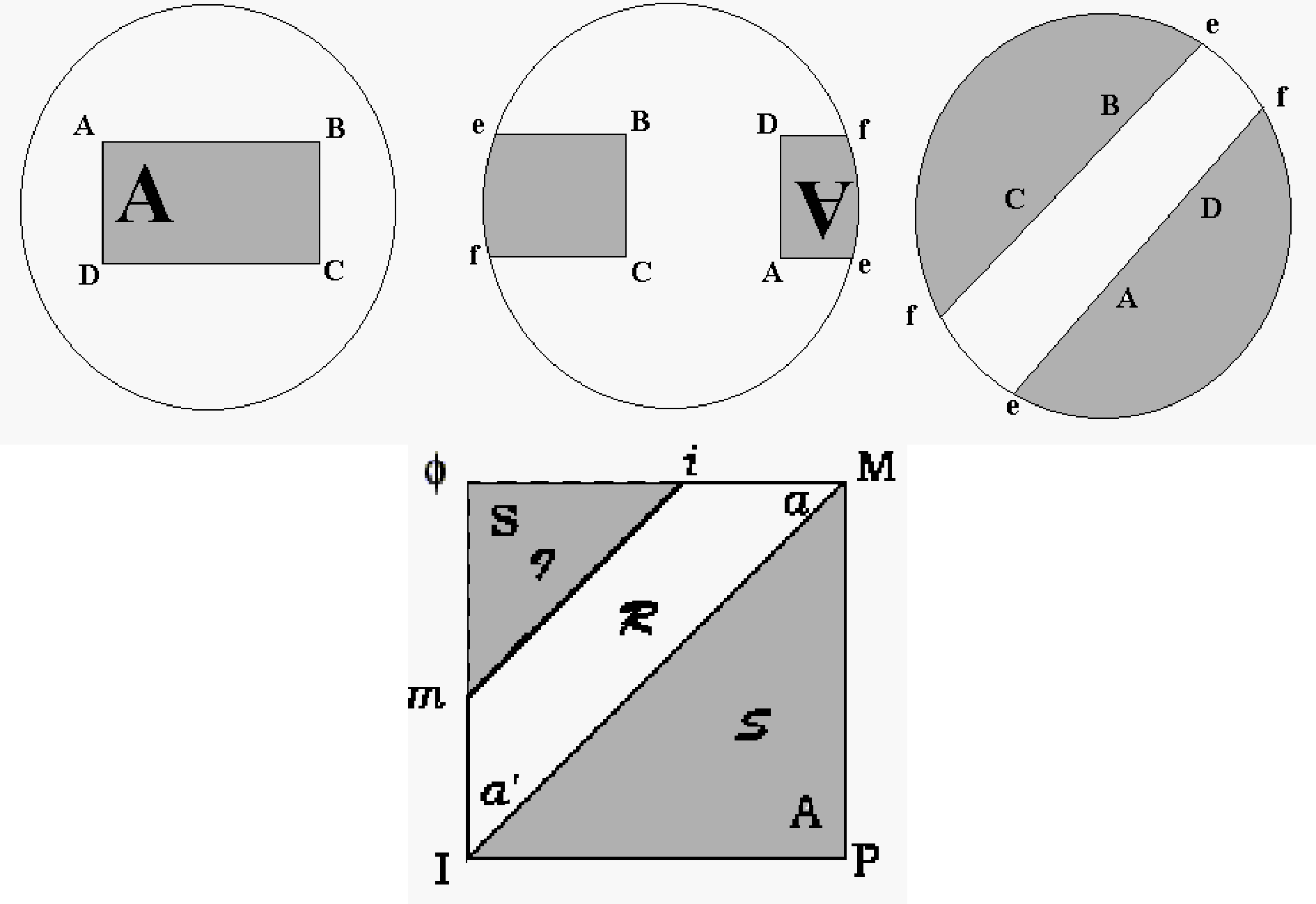
| Figure 5 : Passage progressif par changement de point de vue d’une figure représentant un tableau (non moebien) découpé dans un plan projectif au schéma R de Lacan |
Une autre conséquence importante de l’invention du plan projectif par Desargues, est la possibilité de déplacer le point de vue de la perspective, ou encore, ce qui revient au même, de faire tourner le plan du tableau, déformant ainsi la figure qui y est inscrite, mais sans en modifier les propriétés spécifiquement projectives. Ce déplacement peut s’illustrer en adoptant la représentation du plan projectif par un cercle dont les points diamétraux sont identifiés. On peut alors voir que la figure représentant un tableau ABCD (figure 5) dans un plan projectif peut parfaitement se déformer par simple changement de point de vue, c’est à dire par un simple glissement, en une figure exactement superposable au schéma R de Lacan. Ce changement de point de vue nous montre ainsi un tableau scindé entre une « partie imaginaire », et une « partie symbolique » qui se répartissent de part et d’autre de la partie moebienne du schéma R, supposée s’identifier à la réalité du sujet. Le cadre du tableau vient, lui, s’identifier à la coupure subjective, la structure en double boucle étant ici une conséquence du changement de point de vue. La nature de plan projectif du schéma R, que Lacan souligne dans une note des Ecrits datant précisément de l’année du séminaire « l’objet de la psychanalyse » me semble ainsi plus facile à appréhender.